Inverse Functions à la Emily Alman

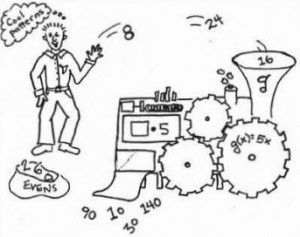In her blog post, My Backwards Approach to Inverse Functions, Emily Alman makes an observation that is, I think, vitally important for math teachers to understand: “One problem with algebra is that there is often a disconnect between the meaning/understanding and the computations/doing. We try our darndest to bridge the gap between the two, but I find that the meaning often gets muddied by cumbersome symbolic computations.” She follows this observation with a fabulous outline of an approach to teaching inverse functions which includes a wonderfully instructive and amusing comic.

I used the comic as homework in my precalculus class this year prior to our first class on inverse functions. To make sure everyone was familiar with the cultural context of the comic, we did the  “Hi, my name is Joe . . . ” skit(?) together in class first. Lots of fun! (Don’t make the mistake of assuming high school students are too old for this. My class had a great time with it. I’ve provide a video link at the bottom of this post in case you’re not familiar with the idea, but don’t show the video in class, DO IT!) Before photocopying the comic and distributing it to students, I filled in functions for the first three “create your own function machines” on the last page so that students would all be finding inverses for the same three functions to start. They created their own functions for the last machine. Along with the comic, the homework included this sheet of instructions (Word version) and a link to a GeoGebraTube exploration from Taylor Russell on graphs of functions and their inverses.

By the time we arrived at the idea that you could find the inverse function by switching x and y and solving for y, most students were excited to have a “shortcut” method for finding an inverse function, as up until then they had been figuring out inverse functions by pure logic. (It reminded me somewhat of the reaction that calculus students have when they discover the power rule when they discover the power rule after days of calculating derivatives of power functions using the limit definition of the derivative.)

As we subsequently worked through the nitty-gritty of inverse functions it became clear that the comic in combination with the process of finding inverse functions using logic had done a great job of establishing the central idea that \(f\left ( f^{-1}\left ( x \right ) \right )=x\). Similarly the GeoGebra piece had done a good job of establishing both the fact that functions and their inverses are symmetric about the line y = x and the rationale for why this should be the case.

[embedit snippet=”hi-my-name-is-joe”]